Senin, 17 Desember 2012

Metode Newton

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Langsung ke: navigasi, cari
Dalam analisis numerik, metode Newton (juga dikenal sebagai metode Newton-Raphson), yang mendapat nama dari Isaac Newton dan Joseph Raphson, merupakan metode yang paling dikenal untuk mencari hampiran terhadap akar fungsi riil. Metode Newton sering konvergen dengan cepat, terutama bila iterasi dimulai "cukup dekat" dengan akar yang diinginkan. Namun bila iterasi dimulai jauh dari akar yang dicari, metode ini dapat meleset tanpa peringatan. Implementasi metode ini biasanya mendeteksi dan mengatasi kegagalan konvergensi.
Diketahui fungsi ƒ(x) dan turunannya ƒ '(x), kita memulai dengan tebakan pertama, x0 .   Hampiran yang lebih baik x1 adalah
x_{1} = x_0 - \frac{f(x_0)}{f'(x_0)}.\,\!

Deskripsi metode

Ilustrasi salah satu iterasi metode Newton (fungsi ƒ ditunjukkan dengan warna biru dan garis singgung dalam warna merah). Kita melihat bahwa xn+1 adalah hampiran yang lebih baik daripada xnuntuk akar x dari fungsi f.
Gagasan metode ini adalah sebagai berikut: kita memulai dengan tebakan awal yang cukup dekat terhadap akar yang sebenarnya, kemudian fungsi tersebut dihampiri dengan garis singgungnya (yang dapat dihitung dengan alat-alat kalkulus, dan kita dapat menghitung perpotongan garis ini dengan sumbu-x (yang dapat dilakukan dengan mudah menggunakan aljabar dasar). Perpotongan dengan sumbu-x ini biasanya merupakan hampiran yang lebih baik ke akar fungsi daripada tebakan awal, dan metode ini dapat diiterasi.
Misalkan ƒ : [a, b] → R adalah fungsi terturunkan yang terdefinisi pada selang [a, b] dengan nilai merupakan bilangan riil R. Rumus untuk menghampiri akar dapat dengan mudah diturunkan. Misalkan kita memiliki hampiran mutakhir xn. Maka kita dapat menurunkan hampiran yang lebih baik, xn+1 dengan merujuk pada diagram di kanan. Kita tahu dari definisi turunan pada suatu titik bahwa itu adalah kemiringan garis singgung pada titik tersebut, yaitu:
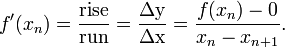
f'(x_{n}) = \frac{ \mathrm{rise} }{ \mathrm{run} } = \frac{ \mathrm{\Delta y} }{ \mathrm{\Delta x} } = \frac{ f( x_{n} ) - 0 }{ x_{n} - x_{n+1} }.\,\!
Di sini, f ' melambangkan turunan fungsi f. Maka dengan aljabar sederhana kita mendapatkan
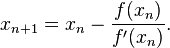
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}. \,\!
Kita memulai proses dengan nilai awal sembarang x0. Metode ini biasanya akan mengerucut pada akar, dengan syarat tebakan awal cukup dekat pada akar tersebut, dan bahwa ƒ'(x0) ≠ 0.
E-to-the-i-pi.svg  Artikel bertopik matematika ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.

         http://id.wikipedia.org/wiki/Metode_Newton  www.iaincirebon.ac.id                                                      

                                            
Diposting oleh di

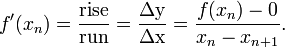
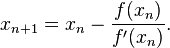
Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)